車両評価の方法と指標
グランツーリスモ7で遊んでいると、車両によって色々な特徴があることを感じますが、自分の感覚が定量的に合っているのか気になります。そこでGT7DashLBoardの取得データを解析して車両評価に挑戦してみます。
関連ページのリンク
- GT7 Dashboardでテレメトリーデータを取得
- GT7DashboardのJSONデータをC#で解析してみた
- 自作ソフトでGT7Dashboardの色々なデータをトレースした
- GT7DashBoardのデータで車両解析する←この記事
車両評価で注目する要素
自動車の走行性能の指標として、加速、最高速、制動、旋回、燃費を挙げることが出来ます。
加速性能の評価方法
一口に加速と言っても低速域から中速域への到達が速い車、中速域からの伸びが優れた車があるかもしれませんが、とりあえず速度域によらず最大加速度を指標の一つとします。
ただ、最大の加速性能だけだと本来の車両のポテンシャルを誤認してしまうかもしれないので、平均加速度を定義します。
平均加速度という概念
加速度は最高速度に近づくと小さくなります。そこで最高速度の90%に到達するまでの加速性能で平均加速度を定義します。平均加速度は「フルスロットルかつ最高速度の90%未満」の条件で走行データを抜き取り、加速度の平均値を求めた値となります。この平均加速度も指標の一つとします。
制動(ブレーキ)性能の評価方法
制動性能は最大加速度とは逆に加速度が最も小さい値をそのまま性能指標とします。
旋回性能の評価方法
旋回運動はヨー角速度で表現します。これは平たく言うと車両の進行方向が変化する速度です。このヨー角速度と車両速度から側面加速度(=横G)を推測可能です。横方向の加速度を正確に測定するには実車両で走行中にGセンサーを用いて測定する必要がありますが、今回はデータから推測し、旋回性能の指標とします。計算方法は少しややこしいので後述します。
燃料消費量
最後は運動性能ではありませんがレースでは重要となる燃費です。走行性能に関してはフリー走行のデータをベースに解析するのがベターですが、燃料消費量だけは実際のレースのデータを取得する必要があります。
GT7Dashboardデータの問題点
早速車両解析を始めたいところですが、ヨー角速度データに問題があるため補正データを作成するプログラムを作成します。
data_rotation_yawの意味
このデータはスタート地点の向きを0として-1~1の値で記録されます。物理学的には回転角は-π~πで表すので、正規化されたような形となります。問題はサーキットはスタート地点から一周して戻ってくるのでスタート時は0、ゴール地点では2(あるいは-2)という値をとりますが、GT7Dashboardでは1を超えるとその超過分を-1に加算した値に補正されます。同様に-1を下回ると-1を下回った分が1に加算した値に補正されます。そのため、データが不連続になり、「fig1.data_rotation_yaw生データ例」となります。

fig1.data_rotation_yaw生データ例
Yaw関連データの補正を行う
生データでは解析に支障があるため、data_rotation_yawの要素から算出した変化量(dYaw)の値が1.9を上回るか、-1.9を下回る場合補正値を加算することでデータを補正します。以下、C#のメソッド例です。
public void CorrectionsYawData()
{
double CorrectionValue = 0;
double dYaw = 0;
double dTime = 0;
if (DataTime.Count() > 1)
{
for (int i = 1; i < DataTime.Count(); i++)
{
DataRotationYaw[i] += CorrectionValue;
dYaw = DataRotationYaw[i] - DataRotationYaw[i - 1];
dTime = DataTime[i] - DataTime[i - 1];
if(dYaw > 1.9)
{
CorrectionValue += -2;
DataRotationYaw[i] += -2;
}
else if (dYaw < -1.9)
{
CorrectionValue += 2;
DataRotationYaw[i] += 2;
}
dYaw = DataRotationYaw[i] - DataRotationYaw[i - 1];
DataAbsoluteYawRatePerSecond[i] = dYaw * Math.PI / dTime;
}
}
}
この補正メソッドを実行することでデータが下図のように補正されます。なお補正後のヨー角速度はπの積をとることでさらにradに補正しています。補正後のデータを
「fig2.data_rotation_yaw補正データとヨー各速度」に示します。
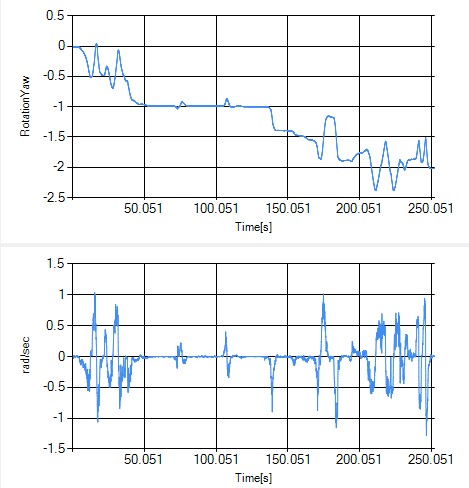
fig2.data_rotation_yaw補正データとヨー各速度
この補正により旋回性能の指標を計算できるようになりました。
旋回性能(横G)の推測方法
横Gを計算には補正したヨー角速度と車両速度を使用します。
理想的な車両の横G計算
まずは単純な物理学に従った理想状態の横Gを求めます。理想状態とは「車両の進行方向と向きが一致した状態」とします。fig.3のようにヨー角速度と車両速度の積で導出可能です。

fig.3 理想車両の側面加速度計算
理想的な車両と実際の車両の違い
先ほど理想状態とは「車両の進行方向と向きが一致した状態」としましたが、実際にはカーブの途中などでは車両の進行方向と車両の向きは一致しません。これは限界に近い領域でより顕著になります。
理想車両の計算式だと横Gが過大になる
限界領域では車両がオーバーステアを出した際にヨー角速度が瞬間的に増大します。この時、すぐにカウンターをあてることで姿勢を進行方向に戻しますが、オーバーステアが発生した瞬間のヨー角速度は実際の進行方向変化に加えてはるかに大きい値となります。fig.4はWRX Gr.3のデータですが、ピークで5.7G程度の値を示しています。横GはF1車両で5G程度なので明らかに過大です。
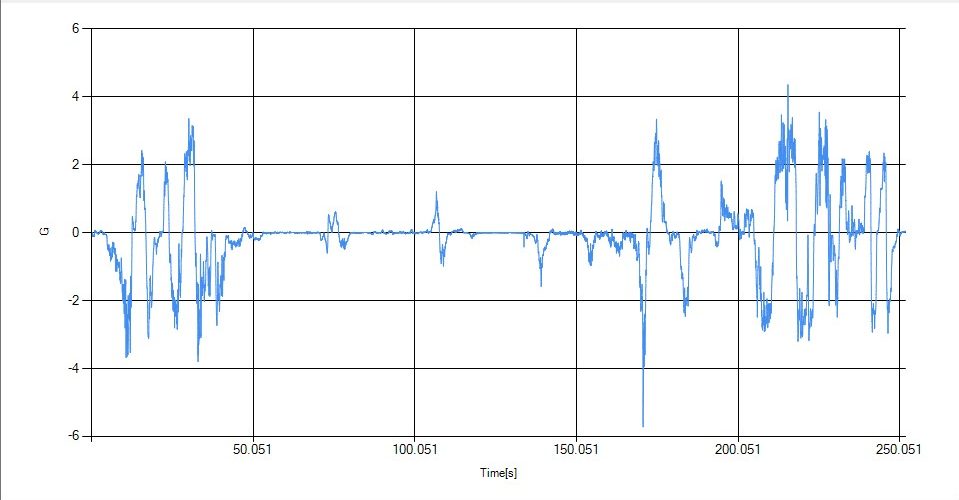
fig.4 WRX Rr.3 HN.G
移動平均フィルタで実際の加速度に近づける
厳密に横Gを求めるのは難しそうなので、ヨー角速度に移動平均フィルタをかけた値で近似値としてみます。実車両のデータから1000ms程度のフィルターが適切と思い、fig.5に出力してみました。横Gは最大3.16程度と実際のGT3車両に近い値ではないかと思います。
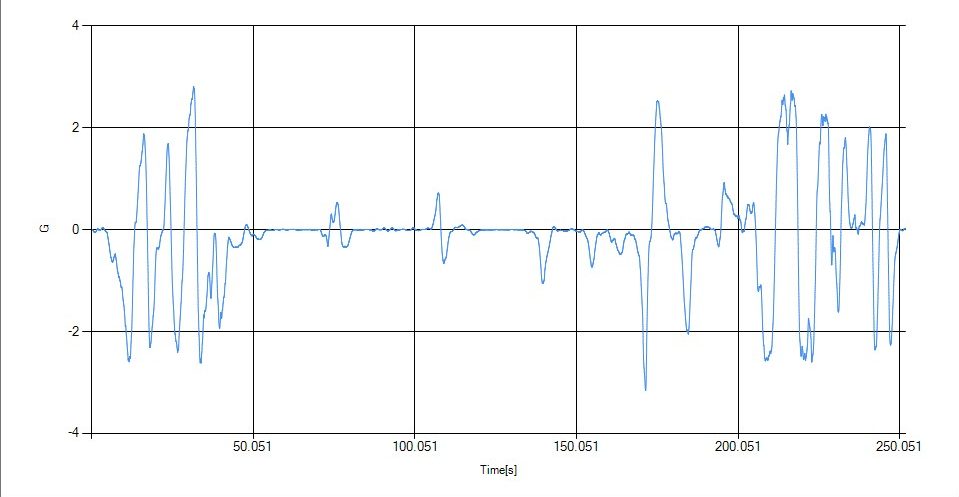
fig.5 WRX Gr.3 HN.G(Moving Average 1s)
移動平均フィルタは1000msで適切か?
これについてはわからないですが、それっぽい値が出たので、しばらくはこの値で分析したいと思います。
実際に車両比較してみる
GT3及びGr.3車両とGr.1車両を比較してみます。
舞台はル・マン24時間サーキット(サルトサーキット)
このコースは序盤は中低速コーナーが続き、中盤は長いストレートとシケインで加速性能とブレーキング性能が試されます。終盤は高速コーナーが続くため旋回性能が試されます。そのため、高性能車両の性能確認を十分に行えるサーキットを言えるでしょう。
エントリー車両
- TS050-Hybrid '16(Gr.1)
- FT-1 VGT GT3
- WRX Gr.3
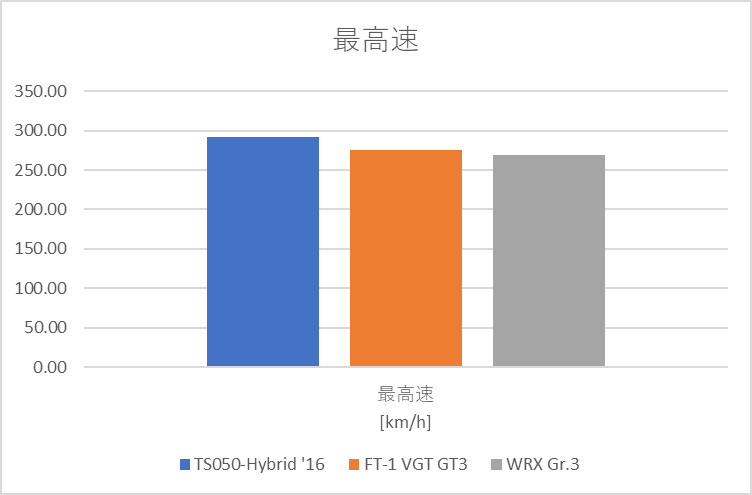
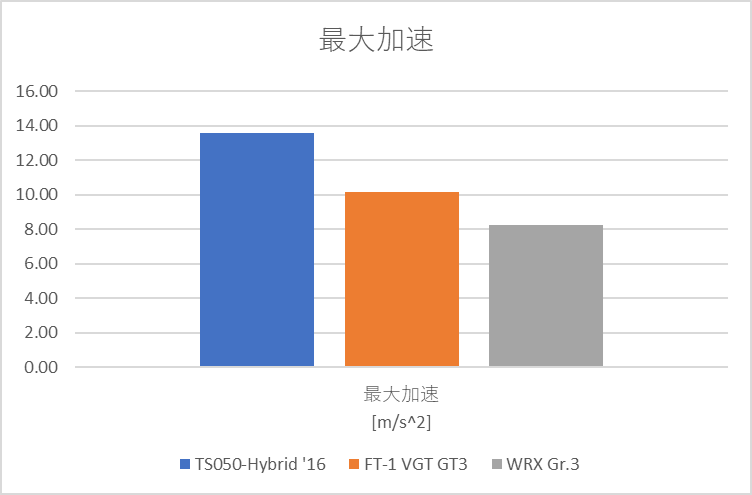
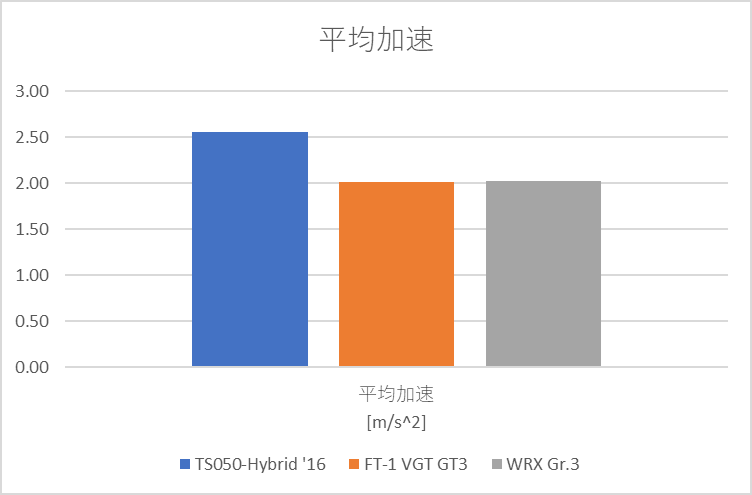
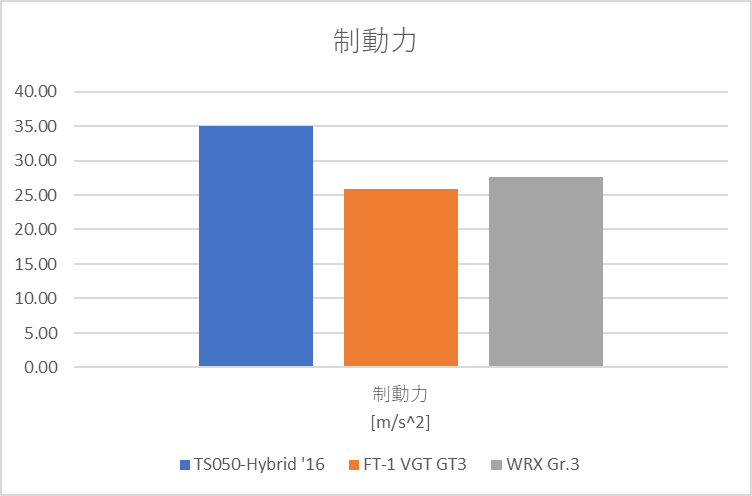
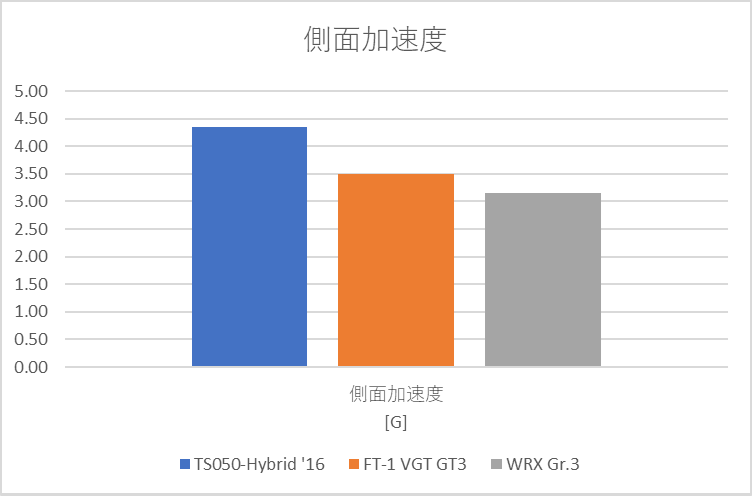
評価結果
やはりGr.1車両は圧倒的に高い性能を誇ります。特に旋回性能が顕著で高速コーナーの旋回速度が圧倒的に高いようです。FT-1とWRXを比較すると、旋回性能はFT-1が高いですが、制動力はWRXが上です。また、最大加速はFT-1の方が明らかに高いですが、平均加速はWRXの方が高いことから、WRXのエンジンがフラットで扱いやすい性能であることが読み取れました。
位置情報と速度から横Gを計算する(2024/11/19追記)
YawRateから横Gを導出してみましたが、やはり本来の値とは異なるので、位置情報から導出してみます。
車両の旋回角速度を位置情報から求める
下の概略図と計算式のようにデータからXY平面上の旋回角速度を求めるには、「現在の位置」、「一つ前の時刻の位置」、「二つ前の時刻の位置」が必要です。
arctanの計算が必要ですが、コンピュータによる計算を行えば一瞬で計算可能です。
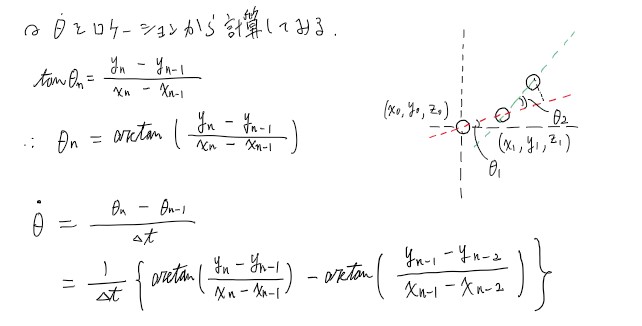
C#で計算してグラフ化してみる
下記のようなメソッドで計算してみた。GT7dashboradではY座標が高低差を表すので、水平方向の加速度はX-Z位置座標を使って計算します。
public void GenRotationGravity()
{
GenPositionDelta();
DataRotationGravity = new List<double>();
DataRotationGravity.Add(0);
if(DataPositiondX.Count == DataTime.Count && DataPositiondZ.Count == DataTime.Count)
{
for (int i = 1; i < DataTime.Count; i++)
{
if (DataPositiondX[i] != 0 && DataPositiondZ[i] != 0 && DataPositiondX[i - 1] != 0 && DataPositiondZ[i - 1] != 0)
{
double dt = DataTime[i] - DataTime[i - 1];
double radSpeed = 1 / dt *
(Math.Atan(DataPositiondZ[i] / DataPositiondX[i]) - Math.Atan(DataPositiondZ[i - 1] / DataPositiondX[i - 1]));
DataRotationGravity.Add(DataSpeed[i] * radSpeed / 3.6 / 9.8);
}
else
{
DataRotationGravity.Add(0);
}
}
}
}
この結果をグラフに描画してみたが、所々でおかしな特異点があるようです。これはarctanの計算仕様によるもので、原因と対処法を考えてみます。
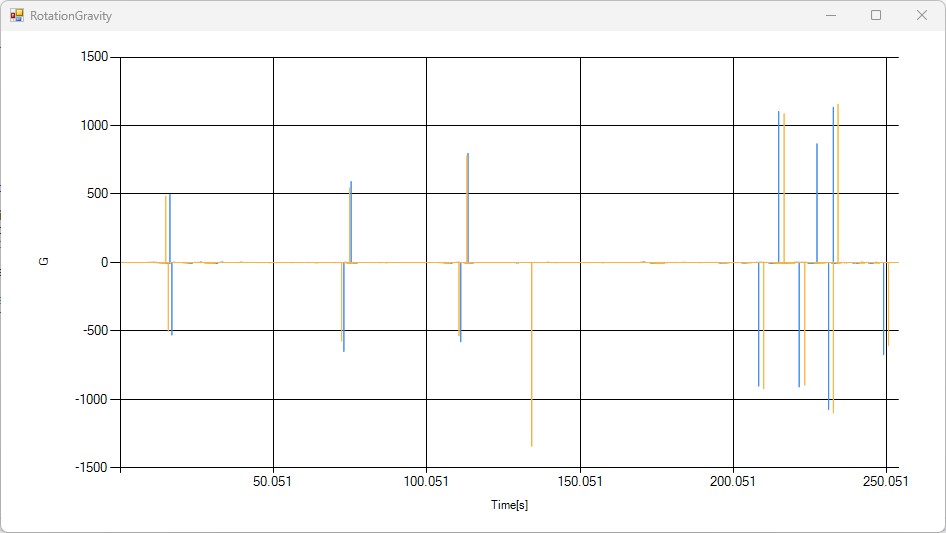
特異点の原因
C#のMath.Atanの説明を見ると出力範囲が-π~πとなっています。そのため、座標が変化して-πより小さい値となると値がπ付近の値に飛ぶことが予想できます。
特異点の対処法
- 今回と前回の角度の差が-π/2を下回った場合、計算値にπを加算する補正を行います。
- 今回と前回の角度の差がπ/2を上回った場合、計算値からπを減算する補正を行います。
実際に下記のようにメソッドのコードを書き換えました。
public void GenRotationGravity()
{
GenPositionDelta();
DataRotationGravity = new List<double>();
DataRotationGravity.Add(0);
if(DataPositiondX.Count == DataTime.Count && DataPositiondZ.Count == DataTime.Count)
{
List<double> radspeedList = new List<double>();
for (int i = 1; i < DataTime.Count; i++)
{
if (DataPositiondX[i] != 0 && DataPositiondZ[i] != 0 && DataPositiondX[i - 1] != 0 && DataPositiondZ[i - 1] != 0)
{
double dt = DataTime[i] - DataTime[i - 1];
double rad = Math.Atan(DataPositiondZ[i] / DataPositiondX[i]) - Math.Atan(DataPositiondZ[i - 1] / DataPositiondX[i - 1]);
if(rad > Math.PI / 2)
{
rad -= Math.PI;
}
else if(rad < -Math.PI / 2)
{
rad += Math.PI;
}
double radSpeed = rad / dt;
DataRotationGravity.Add(DataSpeed[i] * radSpeed / 3.6 / 9.8);
radspeedList.Add(radSpeed);
}
else
{
DataRotationGravity.Add(0);
}
}
}
}
補正した結果
物理的に忠実に求めた結果で良さそうな値が出るようになりました。一か所4Gを超えている部分があるので気になります。
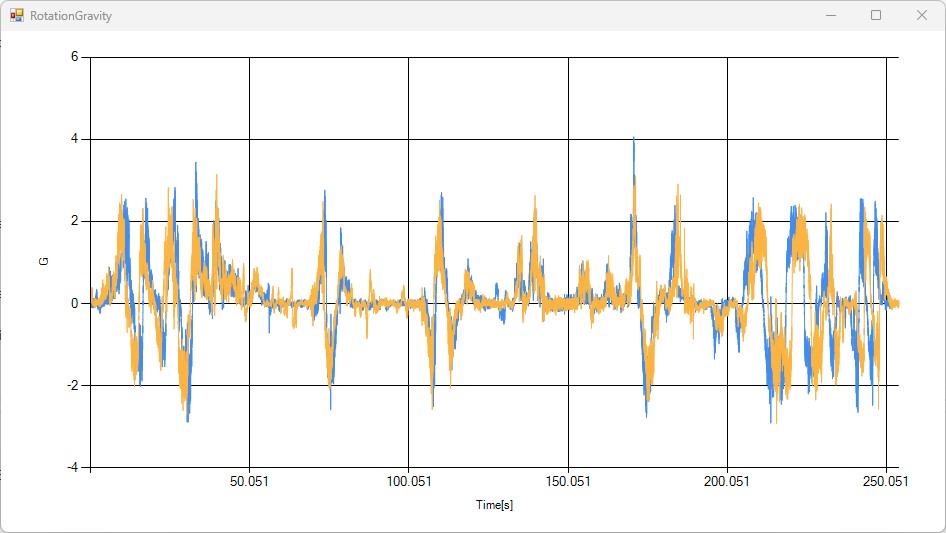
移動平均で補正する
位置情報から横Gを導出する計算は物理法則に忠実ではあるのですが、車両評価という観点で見ると16ms間隔の瞬時データで判定するのは過敏すぎる気がします。
移動平均をかけられるようにする
100msで移動平均をかけられるように機能追加してみました。データ数にすると6個程度になります。ピークが若干抑えられました。
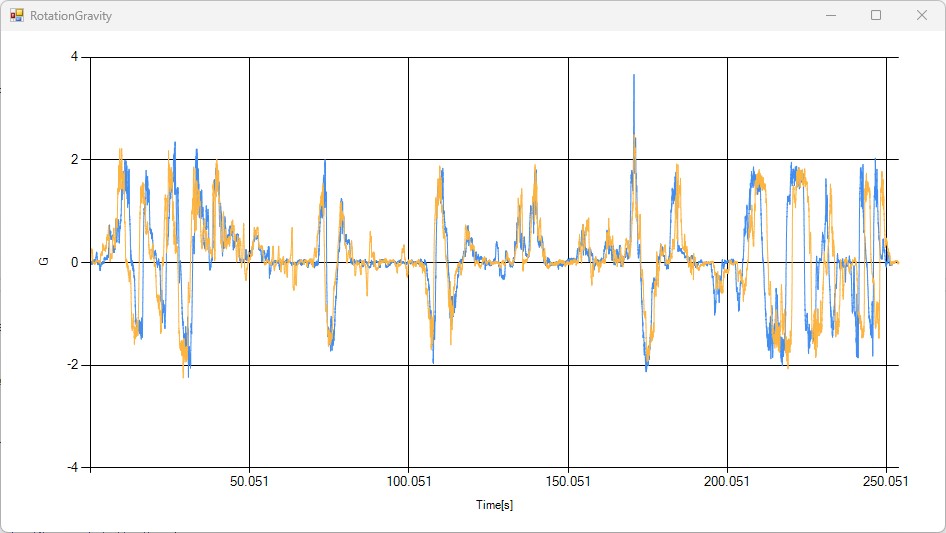
今後の車両評価では100msのフィルターを使う
100ms程度であれば車両の特性を表すデータになるのではないのでしょうか。これから色々な車両データで試してみたいと思います。



